अथ रेखागणितं प्रारभ्यते ।
तत्रास्मिन् ग्रंथे पञ्चदशाध्याया अष्टसप्तत्युत्तरचतु:शतं क्षेतराणि सन्ति । तत्र प्रथमाध्यायेऽष्टचत्त्वारिंशत् क्षेत्राणि प्रदर्श्यन्ते ,,
तत्र आदौ परिभाषा ,
य: पदार्थो दर्शनयोग्यो विभागानर्ह: स बिन्दुशब्दवाच्य: ।
य: पदार्थो दीर्घो विस्ताररहितो विभागार्ह: स रेखाशब्दवाच्य: ।
यैश्र्च विस्तारदैरघ्याभ्यां भिद्यते तद् धरातलक्षेत्रसंज्ञं भवति ।
अथ रेखापि द्विविधा । एका सरला अन्या वक्रा ।
अथ सरलरेखालक्षणम् ।
यस्यां न्यस्ता बिन्दवोऽवलोकिता: सन्त एकबिन्दुनाच्छादिता इव दृश्यन्ते सा सरला रेखा ज्ञायान्यथा कुटिला ।
अथ धरातलक्षेत्रमपि द्विविधम् ।
एकं जलवत् समं द्वितीयं विषमम् । तद्यथा । बिन्दून् लिखित्वा सूत्रं नि:सारयेत् तद्यदि सर्वत्र संलग्नं स्यात्तदा तद् धरातलं समं ज्ञेयमन्यथा विषमम् ।
अथ कोणलक्षणम् ।
धरातले रेखाद्वयोगात् सूच्युत्पद्यते सैव कोण:।
स च द्विविध: समो विषमश्र्च । तौ यथा । समानरेखायां लम्बयोगादुत्पन्नौ कोणौ प्रत्येकम सम कोणौ भवत: रेखे च मिथो लम्बरूपे स्त: ।
अथोल्लीदशाख्यं रेखागणितं लिख्यते ।
तत्र समकोणाल्यूनोऽल्पकोणो भवति ।
समकोणादधिकोऽधिककोणो भवति ।
समातिरिक्तो विषमकोणो भवति ।
इह समकोण: सरलरेखाभ्यामेव भवति ।
विषमकोण: सरलरेखाभ्यां सरलकुटिलरेखाभ्यां कुटिलरेखाभ्यां च भवति ।
अथ क्षेत्रलक्षणम् ।
तत्र धरातलं रेखया रेखाभ्यां रेखाभिर्वा वृतं क्षेत्रसंज्ञं भवति ।
तश्र्च वृत्तलोदण्डत्र्यस्रादिभेदेन बहुभेदं ज्ञेयम् ।
अथ वृत्तलक्षणमम् ।
समधरातले बिन्दुं कृत्वा तस्मात् समानि सूत्राणि सर्वत: कृुत्वा चक्राकौरा कुटिला रेखा कारया सा समानान्तरेण बिन्दुत: सूत्राणं स्पर्शं करिष्यति सैव वृत्तसंजा भवति ।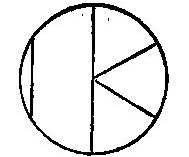
तदाक्रान्तं धरातलं वृत्तक्षेत्रं भवति ।





